Answer:
The solution of this expression is
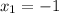 and
and
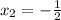 .
.
Explanation:
The procedure for solution of exercise A is described below:
1) We expand the expression.
2) The resulting expression is rearranged into the form of a second order polynomial.
3) Roots are found by Quadratic Formula.
Step 1:
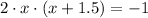
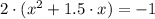
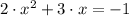
Step 2:
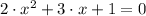
Step 3:
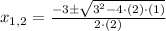
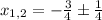
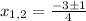
The solution of this expression is
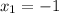 and
and
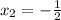 .
.