Answer:

Explanation:
We are asked to find the length of the rake.
We know it hits the wall 80 inches above the ground and the bottom of the rake is 18 inches away from the wall. The point where the top of the rake hits the wall and the distance away from the wall are the legs that form a right angle and the rake is the hypotenuse.
We want to find the hypotenuse or the length of the rake. We will use the Pythagorean Theorem.

In this theorem, a and b are the legs and c is the hypotenuse.
The length of the legs are 80 inches (distance from ground to top of rake) and 18 inches (distance from wall to bottom of rake). The hypotenuse is unknown.
Substitute the known values into the formula.
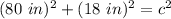
Solve the exponents.
- (80 in)²= 80 in*80 in= 6400 in²
- (18 in)²= 324 in²
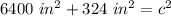
Add.
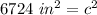
We are solving for c, the hypotenuse, so we must isolate the variable. It is being squared. The inverse of a square is a square root, so we take the square root of both sides.
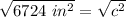
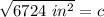
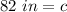
The length of the rake is 82 inches.