Question

(x)=4log(x+2) Which interval has the smallest average rate of change in the given function? 1≤x≤3 5≤x≤7 3≤x≤5 −1≤x≤1

Answer 1

5≤x≤7

Explanation:

For a given function f(x), the average rate of change in a given interval:

a ≤ x ≤ b

is given by:

`r = (f(b) - f(a))/(b - a)`

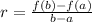
Here we have:

f(x) = 4*log(x + 2)

And we want to see which interval has the smallest average rate of change, so we just need fo find the average rate of change for these 4 intervals.

1) 1≤x≤3

here we have:

`r = (f(3) - f(1))/(3 - 1) = (4*log(3 + 2) - 4*log(1 + 2))/(2) = 0.44`

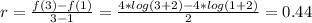
2) 5≤x≤7

`r = (f(7) - f(5))/(7 - 5) = (4*log(7 + 2) - 4*log(5 + 2))/(2) = 0.22`

3) 3≤x≤5

`r = (f(5) - f(3))/(5 - 3) = (4*log(5 + 2) - 4*log(3 + 2))/(2) = 0.29`

4) −1≤x≤1

`r = (f(1) - f(-1))/(1 - (-1)) = (4*log(1 + 2) - 4*log(-1 + 2))/(2) = 0.95`

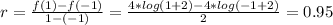
So we can see that the smalles average rate of change is in 5≤x≤7