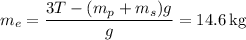Question

A uniform 41.0 kg scaffold of length 6.6 m is supported by two light cables, as shown below. A 74.0 kg painter stands 1.0 m from the left end of the scaffold, and his painting equipment is 1.4 m from the right end. If the tension in the left cable is twice that in the right cable, find the tensions in the cables (in N) and the mass of the equipment (in kg). (Due to the nature of this problem, do not use rounded intermediate values in your calculations—including answers submitted in WebAssign.)

Answer 1

Explanation:

Let

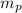`m_p` = mass of the painter

`m_s` = mass of the scaffold

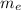`m_e` = mass of the equipment

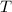`T` = tension in the cables

In order for this scaffold to remain in equilibrium, the net force and torque on it must be zero. The net force acting on the scaffold can be written as

`3T = (m_p + m_s + m_e)g\:\:\:\:\:\:\:(1)`

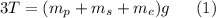
Set this aside and let's look at the net torque on the scaffold. Assume the counterclockwise direction to be the positive direction for the rotation. The pivot point is chosen so that one of the unknown quantities is eliminated. Let's choose our pivot point to be the location of
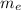`m_e`. The net torque on the scaffold is then

`T(1.4\:\text{m}) + m_sg(1.9\:\text{m}) + m_pg(4.2\:\text{m}) - 2T(5.2\:\text{m}) = 0`

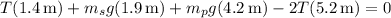
Solving for T,

`9T = m_sg(1.9\:\text{m}) + m_pg(4.2\:\text{m})`

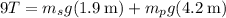
or

`T = (1)/(9)[m_sg(1.9\:\text{m}) + m_pg(4.2\:\text{m})]`

`\:\:\:\:= 423.3\:\text{N}`

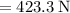
To solve for the the mass of the equipment
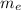`m_e`, use the value for T into Eqn(1):

`m_e = (3T - (m_p + m_s)g)/(g) = 14.6\:\text{kg}`