Gina charges $
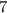 per hour for babysitting with an initial fee of $
per hour for babysitting with an initial fee of $
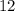 .
.
To find the initial fee and hourly fee, you can use the information provided in the table to set up a system of equations.
Let h be the hourly fee and i be the initial fee.
Given data points:
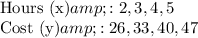
The general formula for the cost y in terms of x, h, and i is:
![\[ y = h \cdot x + i \]](https://img.qammunity.org/2022/formulas/mathematics/college/vfn9l1657jxbekqo8vmluoppersa8q7nzl.png)
Now, substitute the values from the table into this formula to create a system of equations:
1. For
![\( x = 2 \), \( y = 26 \):\[ 26 = 2h + i \]](https://img.qammunity.org/2022/formulas/mathematics/college/te2l17ga3sg2rv71oeie83yfd1imiet1f3.png)
2. For
![\( x = 3 \), \( y = 33 \):\[ 33 = 3h + i \]](https://img.qammunity.org/2022/formulas/mathematics/college/kkr4mvf24rd6zqivf6rd5e92enq2rayh6f.png)
3. For
![\( x = 4 \), \( y = 40 \):\[ 40 = 4h + i \]](https://img.qammunity.org/2022/formulas/mathematics/college/fn6jqgu2r75bwxjjje9b565zyzxu1p8au6.png)
4. For

Now, you have a system of four equations:
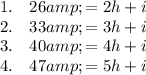
Here's one way to solve it:
Subtract equation (
 ) from equation (
) from equation (
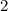 ):
):
![\[ (2) - (1) \implies 33 - 26 = (3h + i) - (2h + i) \]\[ 7 = h \]](https://img.qammunity.org/2022/formulas/mathematics/college/yxrx2vfd7ebbeodomz7hhdnx3swut3mk1z.png)
Now that we know h =
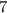 , substitute this value into any of the original equations. Let's use equation (
, substitute this value into any of the original equations. Let's use equation (
 ):
):
![\[ 26 = 2(7) + i \]\[ 26 = 14 + i \]\[ i = 26 - 14 \]\[ i = 12 \]](https://img.qammunity.org/2022/formulas/mathematics/college/jm6up6wk8nknkurmf4e6acyrfn3wkthojy.png)
So, the solution to the system is
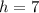 (hourly fee) and
(hourly fee) and
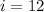 (initial fee). Therefore, Gina charges $
(initial fee). Therefore, Gina charges $
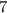 per hour for babysitting, and there is an initial fee of $
per hour for babysitting, and there is an initial fee of $
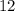 .
.