Question

An object is made of glass and has the shape of a cube 0.13 m on a side, according to an observer at rest relative to it. However, an observer moving at high speed parallel to one of the object's edges and knowing that the object's mass is 3.3 kg determines its density to be 8100 kg/m3, which is much greater than the density of glass. What is the moving observer's speed (in units of c) relative to the cube

Answer 1

`v=0.9833\ c`

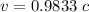
Step-by-step explanation:

The density changes means that the length in the direction of the motion is changed.

Therefore,

`$\text{Density} = (m)/(lwh)$`

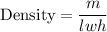
Given :

Side, b = h = 0.13 m

Mass, m = 3.3 kg

Density = 8100
`kg/m^3`

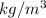
So,

`$8100=(3.3)/(l * 0.13 * 0.13)$`

`$l=(3.3)/(8100 * 0.13 * 0.13)$`

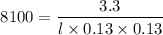
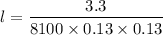
l = 0.024 m

Then for relativistic length contraction,

`$l= l' \sqrt{1-(v^2)/(c^2)}$`

`$0.024= 0.13 \sqrt{1-(v^2)/(c^2)}$`

`$0.184= \sqrt{1-(v^2)/(c^2)}$`

`$0.033= 1-(v^2)/(c^2)}$`

`$(v^2)/(c^2)= 0.967$`

`$(v)/(c)=0.9833$`

`v=0.9833\ c`

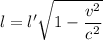
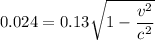
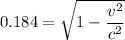
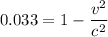
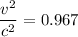
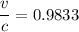
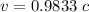
Therefore, the speed of the observer relative to the cube is 0.9833 c (in the units of c).