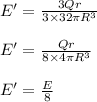Answer:
The electric field is E/8.
Step-by-step explanation:
The electric field due to a solid sphere of uniform charge density inside it is given by
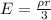
where,
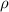 is the volume charge density and r is the distance from the center.
is the volume charge density and r is the distance from the center.
For case I:
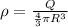
So, electric field at a distance r is
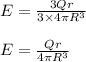
Case II:
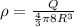
So, the electric field at a distance r is