Answer:
The final velocity of the lion-gazelle system is approximately 62.321 kilometers per hour.
Step-by-step explanation:
Let suppose that both lion and the Thomson's gazelle collide each other inelastically, the use of the Principle of Linear Momentum Conservation suffices to describe the entire phenomenon:
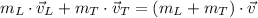 (1)
(1)
Where:
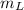 - Mass of the lion, in kilograms.
- Mass of the lion, in kilograms.
 - Mass of the Thomson's gazelle, in kilograms.
- Mass of the Thomson's gazelle, in kilograms.
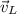 - Initial velocity of the lion, in meters per second.
- Initial velocity of the lion, in meters per second.
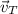 - Initial velocity of the Thomson's gazelle, in meters per second.
- Initial velocity of the Thomson's gazelle, in meters per second.
 - Final velocity of the lion-gazelle system, in meters per second.
- Final velocity of the lion-gazelle system, in meters per second.
Let suppose that both northward velocity and eastward velocity are positive.
If we know that
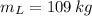 ,
,
![\vec v_(L) = (0, 22.222)\left[(m)/(s) \right]](https://img.qammunity.org/2022/formulas/physics/high-school/aql54hyc652g69j1k9gflie76nqudfoayx.png) ,
,
 and
and
![\vec v_(T) = (21.667, 0)\,\left[(m)/(s) \right]](https://img.qammunity.org/2022/formulas/physics/high-school/dmmt2imggib3gfu77t9sdhwol62zw4vb0y.png) , then the final velocity of the lion-gazelle system is:
, then the final velocity of the lion-gazelle system is:
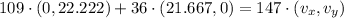
![(v_(x), v_(y)) = (0, 16.478) + (5.306, 0) \,\left[(m)/(s) \right]](https://img.qammunity.org/2022/formulas/physics/high-school/9fu2eo7b2ybcuhpb6vbvtovjno69suiu60.png)
![(v_(x), v_(y)) = (5.306, 16.478)\,\left[(m)/(s) \right]](https://img.qammunity.org/2022/formulas/physics/high-school/v0f66ba11h3kjhnqrtq3q6cc1uncqd4ip6.png)
![(v_(x), v_(y)) = (19.102, 59.321)\,\left[(km)/(h) \right]](https://img.qammunity.org/2022/formulas/physics/high-school/iosvxut11bzhd71m9svcain8h6220sjzks.png)
And the final speed of the lion-gazelle system is calculated by the Pythagorean Theorem:
![v = \sqrt{19.102^(2)+59.321^(2)}\,\left[(km)/(h) \right]](https://img.qammunity.org/2022/formulas/physics/high-school/w8dh6ytbhev3h8mz5e56coh9mn6lgynpy4.png)
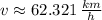
The final velocity of the lion-gazelle system is approximately 62.321 kilometers per hour.