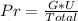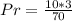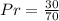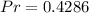Answer:
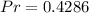
Explanation:
Given
Let
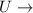 Undergraduates
Undergraduates
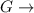 Graduates
Graduates
So, we have:
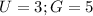 -- Total students
-- Total students
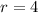 --- students to select
--- students to select
Required
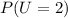
From the question, we understand that 2 undergraduates are to be selected; This means that 2 graduates are to be selected.
First, we calculate the total possible selection (using combination)
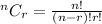
So, we have:
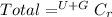
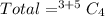
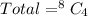
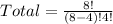
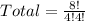
Using a calculator, we have:
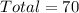
The number of ways of selecting 2 from 3 undergraduates is:
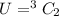
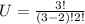
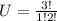
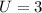
The number of ways of selecting 2 from 5 graduates is:
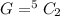
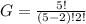
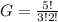
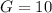
So, the probability is: