Question

Two children (each having a mass of 60 kg) are standing on the edge a merry-go-round (mass of 140 kg) as it spins with an angular velocity of 0.75 rad/s. The two children jump off the merry-go-round. What is the angular velocity of the merry-go-round after the children have jumped off

Answer 1

The angular velocity after the children jump off is approximately 1.4 rad/s

Step-by-step explanation:

The given parameters are;

The masses of each child, m₁, and m₂ = 60 kg

The mass of the merry-go-round, m₃ = 140 kg

The initial angular velocity,
`\omega_i` = 0.75 rad/s

The angular velocity after the children jump off =
`\omega_f`

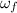
According to the principle of conservation of angular momentum

The angular momentum = I × ω

The moment of inertia, I = m × R²

The total initial angular momentum =
`I_i * \omega_i = m_i * R^2 * \omega_i`

The total angular momentum after the children jump off =
`I_f * \omega_f = m_f * R^2 * \omega_f`

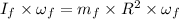
The initial mass,
`m_i` = m₁ + m₂ + m₃ = 60 kg + 60 kg + 140 kg = 260 kg

The final mass,
`m_f` = m₃ = 140 kg

According to the principle of conservation of linear momentum, we have;

`I_i * \omega_i` =
`I_f * \omega_f`

Therefore;

260 kg × R² × 0.75 rad/s = 140 kg × R² ×
`\omega_f`

∴
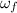
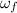`\omega _f` = (260 kg × R² × 0.75 rad/s)/(140 kg × R²) = 1.39285714 rad/s. ≈ 1.4 rad/s

The angular velocity after the children jump off,
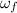`\omega _f` ≈ 1.4 rad/s.