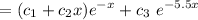Solution :
Given :
2y''' + 15y'' + 24y' + 11y= 0
Let x = independent variable
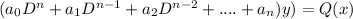 is a differential equation.
is a differential equation.
If
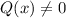
It is non homogeneous then,
The general solution = complementary solution + particular integral
If Q(x) = 0
It is called the homogeneous then the general solution = complementary solution.
2y''' + 15y'' + 24y' + 11y= 0
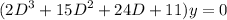
Auxiliary equation,
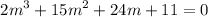
-1 | 2 15 24 11
| 0 -2 - 13 -11
2 13 11 0
∴
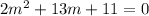
The roots are
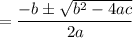
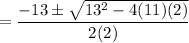
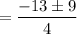
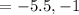
So,
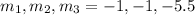
Then the general solution is :