Answer:
Since
 and
and
 , the normal distribution can be used to approximate the binomial distribution.
, the normal distribution can be used to approximate the binomial distribution.
The mean is 13.3 and the standard deviation is 3.28.
Explanation:
Binomial probability distribution
Probability of exactly x successes on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
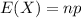
The standard deviation of the binomial distribution is:

Normal probability distribution
Problems of normally distributed distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
When we are approximating a binomial distribution to a normal one, we have that
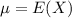 ,
,
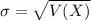 , if
, if
 and
and
 .
.
The probability than an adult never had the flu is 19%.
This means that

You randomly select 70 adults and ask if he or she ever had the flu.
This means that
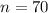
Decide whether you can use the normal distribution to approximate the binomial distribution
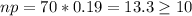

Since
 and
and
 , the normal distribution can be used to approximate the binomial distribution.
, the normal distribution can be used to approximate the binomial distribution.
Mean:
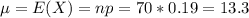
Standard deviation:
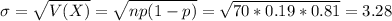
The mean is 13.3 and the standard deviation is 3.28.