Question

A uniform, solid sphere of radius 2.50 cm and mass 4.75 kg starts with a purely translational speed of 3.00 m/s at the top of an inclined plane. The surface of the incline is 2.75 m long, and is tilted at an angle of 22.0∘ with respect to the horizontal. Assuming the sphere rolls without slipping down the incline, calculate the sphere's final translational speed v2 at the bottom of the ramp.

Answer 1

The final translational seed at the bottom of the ramp is approximately 4.84 m/s

Step-by-step explanation:

The given parameters are;

The radius of the sphere, R = 2.50 cm

The mass of the sphere, m = 4.75 kg

The translational speed at the top of the inclined plane, v = 3.00 m/s

The length of the inclined plane, l = 2.75 m

The angle at which the plane is tilted, θ = 22.0°

We have;

`K_i` +
`U_i` =
`K_f` +
`U_f`

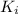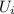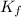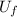
K = (1/2)×m×v²×(1 + I/(m·r²))

I = (2/5)·m·r²

K = (1/2)×m×v²×(1 + 2/5) = 7/10 × m×v²

U = m·g·h

h = l×sin(θ)

h = 2.75×sin(22.0°)

∴ 7/10×4.75×3.00² + 4.75×9.81×2.75×sin(22.0°) = 7/10 × 4.75×
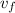`v_f`² + 0

7/10×4.75×3.00² + 4.75×9.81×2.75×sin(22.0°) ≈ 77.93

∴ 77.93 ≈ 7/10 × 4.75×
`v_f`²

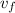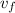`v_f`² = 77.93/(7/10 × 4.75)

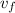`v_f` ≈ √(77.93/(7/10 × 4.75)) ≈ 4.84

The final translational seed at the bottom of the ramp,
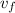`v_f` ≈ 4.84 m/s.