Answer:
a) 0.1287 = 12.87% probability the sample will contain exactly 8 defective drives
b) 0.2092 = 20.92% probability the sample will contain more than 8 defective drives.
c) 0.6621 = 66.21% probability the sample will contain less than 8 defective drives.
d) The expected number of defective drives in the sample is 6.6
Explanation:
For each DVD, there are only two possible outcomes. Either it is defective, or it is not. The probability of a DVD being defective is independent of any other DVD, which means that the binomial probability distribution is used to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
A company that produces DVD drives has a 12% defective rate.
This means that
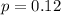
Let X represent the number of defectives in a random sample of 55 of their drives.
This means that

a. What is the probability the sample will contain exactly 8 defective drives?
This is
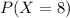 . So
. So

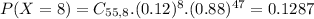
0.1287 = 12.87% probability the sample will contain exactly 8 defective drives.
b. What is the probability the sample will contain more than 8 defective drives?
This is:
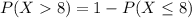
In which:
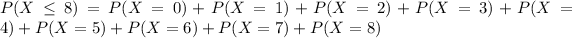
Then

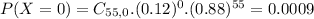
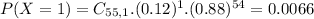
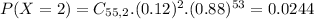
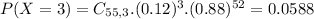
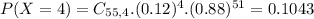
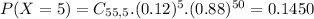
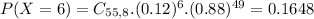
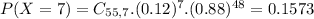
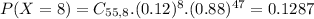
So

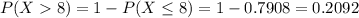
0.2092 = 20.92% probability the sample will contain more than 8 defective drives.
c. What is the probability the sample will contain less than 8 defective drives?
This is:
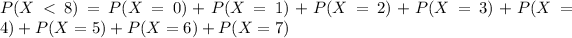
With the values we found in b.
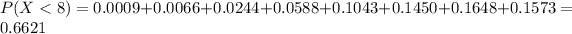
0.6621 = 66.21% probability the sample will contain less than 8 defective drives.
d. What is the expected number of defective drives in the sample?
The expected value of the binomial distribution is:
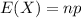
In this question:
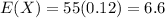
The expected number of defective drives in the sample is 6.6