Question

Two manned satellites approach one another at a relative velocity of v=0.190 m/s, intending to dock. The first has a mass of m1=4.00×103 kg and the second a mass of m2=7.50×103 kg. If the two satellites collide elastically rather than dock, what is their final relative velocity?

Answer 1

Their final relative velocity is 0.190 m/s

Step-by-step explanation:

The relative velocity of the satellites, v = 0.190 m/s

The mass of the first satellite, m₁ = 4.00 × 10³ kg

The mass of the second satellite, m₂ = 7.50 × 10³ kg

Given that the satellites have elastic collision, we have;

`v_2 = (2 \cdot m_1)/(m_1 + m_2) \cdot u_1 - (m_1 - m_2)/(m_1 + m_2) \cdot u_2`

`v_2 = ( m_1 - m_2)/(m_1 + m_2) \cdot u_1 + (2 \cdot m_2)/(m_1 + m_2) \cdot u_2`

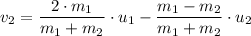
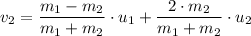
Given that the initial velocities are equal in magnitude, we have;

u₁ = u₂ = v/2

u₁ = u₂ = 0.190 m/s/2 = 0.095 m/s

v₁ and v₂ = The final velocities of the satellites

We get;

`v_1 = (2 * 4.0 * 10^3)/(4.0 * 10^3 + 7.50 * 10^3) * 0.095 - (4.0 * 10^3- 7.50* 10^3)/(4.0 * 10^3+ 7.50* 10^3) * 0.095 = 0.095`

`v_2 = ( 4.0 * 10^3 - 7.50* 10^3)/(4.0 * 10^3 + 7.50 * 10^3) * 0.095 + (2 * 7.50* 10^3)/(4.0 * 10^3+ 7.50* 10^3) * 0.095 = 0.095`

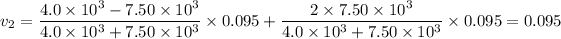
The final relative velocity of the satellite,
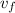`v_f` = v₁ + v₂

∴
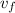`v_f` = 0.095 + 0.095 = 0.190

The final relative velocity of the satellite,
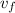`v_f` = 0.190 m/s