Answer:
Their final relative velocity is 0.190 m/s
Step-by-step explanation:
The relative velocity of the satellites, v = 0.190 m/s
The mass of the first satellite, m₁ = 4.00 × 10³ kg
The mass of the second satellite, m₂ = 7.50 × 10³ kg
Given that the satellites have elastic collision, we have;
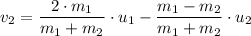
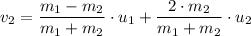
Given that the initial velocities are equal in magnitude, we have;
u₁ = u₂ = v/2
u₁ = u₂ = 0.190 m/s/2 = 0.095 m/s
v₁ and v₂ = The final velocities of the satellites
We get;
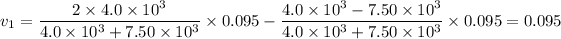
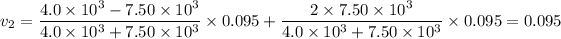
The final relative velocity of the satellite,
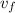 = v₁ + v₂
= v₁ + v₂
∴
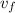 = 0.095 + 0.095 = 0.190
= 0.095 + 0.095 = 0.190
The final relative velocity of the satellite,
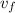 = 0.190 m/s
= 0.190 m/s