Question

A car salesman claims that the variance of prices on convertibles is higher than the variance on station wagons. To test this claim, he selects random samples of each type of car, and records the prices. The standard deviation of 16 convertibles is $6800 and the standard deviation of 24 station wagons is $3900. For , what is the p-value? Group of answer choices

Answer 1

Explanation:

Answer 2

Hence the critical value for the right-tailed test is
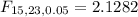`F_(15,23,0.05)=2.1282`. Since the test value is greater than the critical value so we reject the null hypothesis.

Explanation:

Hypotheses are:

`H_(0):\sigma_(1)^(2)=\sigma_(2)^(2)\\H_(a):\sigma_(1)^(2)>\sigma_(2)^(2)`

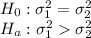
Here we have s_{1}=6800 and s_{2}=3900. Here we will use F -test. The Value of test statistics is

`F=(s_(1)^(2))/(s_(2)^(2))\\\\F=(6800^(2))/(3900^(2))\\\\F=3.0401`

Here the degree of freedom of the numerator is
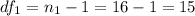`df_(1)=n_(1)-1=16-1=15` and The degree of the denominator is

`df_(2)=n_(2)-1 \\\\=24-1=23 .`

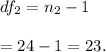
The critical value for the right-tailed test is
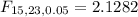`F_(15,23,0.05)=2.1282`. Since the test value is greater than the critical value so we reject the null hypothesis.