Answer:
(i) The particle has a period of 0.3 seconds.
(ii) The angular velocity of the particle is a20.944 radians per second.
(iii) The linear velocity of the particle is 1.047 meters per second.
(iv) The linear acceleration of the particle is 21.933 meters per square second.
Step-by-step explanation:
Statement is incomplete and have mistakes, complete and correct form is presented below:
A particle makes 800 revolutions in 4 minutes of a circle with a radius of 5 centimeters. Find (i) its period, (ii) its angular velocity, (iii) its linear velocity and (iv) its acceleration.
(i) The period of the particle (
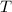 ), in seconds, is the time taken to make a complete revolution:
), in seconds, is the time taken to make a complete revolution:
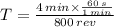
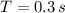
The particle has a period of 0.3 seconds.
(ii) The angular velocity (
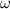 ), in radians per second, is determined by the following formula:
), in radians per second, is determined by the following formula:
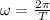 (1)
(1)
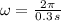

The angular velocity of the particle is a20.944 radians per second.
(iii) The linear velocity (
 ), in meters per second, is calculated by the following formula:
), in meters per second, is calculated by the following formula:
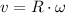 (2)
(2)
Where
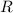 is the radius of the circle, in meters.
is the radius of the circle, in meters.
If we know that
 and
and
 , then the linear velocity of the particle is:
, then the linear velocity of the particle is:
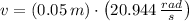
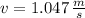
The linear velocity of the particle is 1.047 meters per second.
(iv) Since angular velocity is constant, linear acceleration of the particle (
 ), in meters per square second, is entirely radial. Acceleration can be found by means of this expression:
), in meters per square second, is entirely radial. Acceleration can be found by means of this expression:
 (3)
(3)
If we know that
 and
and
 , then the linear acceleration of the particle is:
, then the linear acceleration of the particle is:
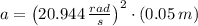
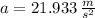
The linear acceleration of the particle is 21.933 meters per square second.