Question

A boy shoves his stuffed toy zebra down a frictionless chute. It starts at a height of 1.45 m above the bottom of the chute with an initial speed of 1.23 m/s . The toy animal emerges horizontally from the bottom of the chute and continues sliding along a horizontal surface with a coefficient of kinetic friction of 0.231 . How far from the bottom of the chute does the toy zebra come to rest? Assume g=9.81 m/s2 .

Answer 1

The answer is "4.97 m".

Step-by-step explanation:

`u = 1.23\ (m)/(s)\\\\`

`H= 1.45 \ m\\\\`

`\mu = 0.231\\\\`

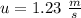
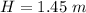
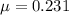
The law of conservation tells us that heat energy at the top with kinetic energy at the top equals kinetic energy at the base.

`mgh+(1)/(2)mu^2=(1)/(2)mv^2\\\\2gh +u^2 =v^2\\\\v=√(u^2+2gh)`

`v=\sqrt{(1.23\ (m)/(s))^2+2(9.81 (m)/(s^2)) +(1.45\ m)`

`=√(1.5129+19.62 +1.45)\\\\=√(22.5829)\\\\=4.75\ (m)/(s)`

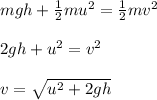
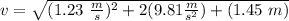
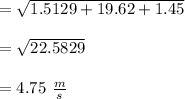
Friction force is given by the formula

`f=-\mu mg \\\\ma= -\mu mg\\\\a=-\mu g\\\\`

`= -(0.231) \ (9.81\ (m)/(s^2))\\\\=-2.26611 \ (m)/(s^2)`

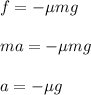
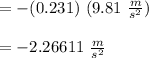
Now by using an equation of motion as

`v^2-u^2= 2as`

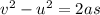
From the above the distance traveled is

`S=(v^2-u^2)/(2a)`

`S=((0)^2-(4.75\ (m)/(s))^2)/(2(-2.26611\ (m)/(s^2)))\\\\`

`=(-(4.75\ (m)/(s))^2)/(2(-2.26611\ (m)/(s^2)))\\\\=(-22.5625)/(-4.53222)\\\\=4.97`

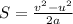
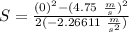
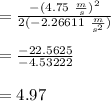
In other words, the distance from the bottom of the chute to the point where the toy zebra comes to rest is
`s = 4.97\ m`