Hi there!
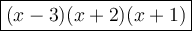
We can use long division to find the other roots of p(x).
We know that x + 1 is a factor, so:
Set up:
Find how many times that the first term in the divisor goes into the first of the dividend. Subtract from like terms.
x² - x - 6
x + 1 | x³ + 0x² - 7x - 6
x³ + x²
0 - x² - 7x
- x² - x
0 - 6x - 6
-6x - 6
0 0
Therefore, x² - x - 6 is another factor. We can factor this further:
Find two numbers that add up to -1 and multiply into -6. We get:
-3, 2
(x - 3)(x + 2)
The entire polynomial factored is:
(x -3)(x + 2)(x + 1)