Answer:
i =
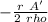 , i = 0.92 A
, i = 0.92 A
Step-by-step explanation:
This exercise asks for the electromotive force, which can be calculated with Faraday's law
fem =
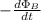
where the magnetic flux
Ф = B. A
bold letters indicate vectors. We can write this equation
Ф = B A cos θ
In this case the magnetic field is perpendicular to the page and the normal to the loop of the loop is also parallel to the page, therefore the angle is zero and the cosine is 1
the loop is
A = π r²
we substitute in the first equation
fem = - π r²
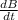
we substitute the values
fem = -π r² 1
fem = - π r²
to calculate the current let's use ohm's law
V = i R
R = ρ L / A'
where A 'is the area of the wire and L is the length of the loop
L = 2π r
V = i (ρ 2π r / A ')
I =
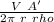
In this case
V = fem
I = fem / R
i =
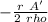
In order to complete the calculation, you need the radius of the loop and / or the wire cutter.
if we assume that the loop has a radius of r = 1 cm = 0.01 m and an area of the wire A'= π 10⁻⁶ m² a radius of the wire 1 mm
i = - 10⁻² π 10⁻⁶ / ( 2 1.7 10-8)
i = 0.92 A