Answer:
Parthava had 100 arrows.
Explanation:
Let's define N as the number of arrows that Parthava originally has.
He uses one-half of them in defending himself, so he used N/2 arrows
Now he uses four times the square root of the number of arrows, so now he uses:
4*√N
Then he uses 6
Then he uses 3
Then he uses the last one.
If we add all these numbers of arrows that he used, we should get the initial number of arrows that he used, then:
N/2 + 4*√N + 6 + 3 + 1 = N
Now we have an equation that we can try to solve.
First, let's move all the terms to the same side:
N/2 + 4*√N + 6 + 3 + 1 - N = 0
now we can simpify it:
(N/2 - N) + 4*√N + (6 + 3 + 1) = 0
-(1/2)*N + 4*√N + 10 = 0
Now we can define a new variable x = √N
Then we have: x^2 = N
now we can replace these new variables in our equation to get:
-(1/2)*x^2 + 4*x + 10 = 0
Now we just have a quadratic equation.
Remember that for a quadratic equation of the form:
0 = a*x^2 + b*x + c
The solutions were given by:

Then in our case, the solutions will be:
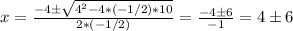
So there are two solutions:
x = 4 + 6 = 10
x = 4 - 6 = -2
And remember that x = √N
Then x should be positive, then we take x = 10 as our solution here.
then we can use the equation:
x = 10 = √N
then
10^2 = √N^2 = N
10^2 = 100 = N
Parthava had 100 arrows.