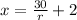Question

The surface area of a cylinder is given by the formula

S = 30πr + 2πr2

How many times greater is this compared to a circle with A = πr2

Answer 1

`x = \frac {30}{r} + 2`

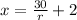
Explanation:

Given the following data;

• S.A of cylinder = 30πr + 2πr²
• Area of circle = πr²

To find how many times greater is the S.A compared to the area, we would have to divide the surface area (S.A) of the cylinder by the area of circle.

Let the unknown variable be x.

`x = \frac {30 \pi r + 2 \pi r^(2)}{\pi r^(2)}`

Factorizing the numerator, we have;

`x = \frac {\pi r(30 + 2r)}{\pi r^(2)}`

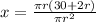
Dividing both sides by πr, we have;

`x = \frac {30 + 2r}{r}`

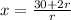
Simplifying further, we would have;

`x = \frac {30}{r} + 2`