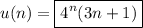I don't know what methods are available to you, so I'll just use one that I'm comfortable with: generating functions. It's a bit tedious, but it works! If you don't know it, there's no harm in learning about it.
Let U(x) be the generating function for the sequence u(n), i.e.

In the recurrence equation, we multiply both sides by xⁿ (where |x| < 1, which will come into play later), then take the sums on both sides from n = 0 to ∞, thus recasting the equation as
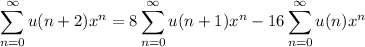
Next, we rewrite each sum in terms of U(x). For instance,

After rewriting each sum in a similar way, we end up with a linear equation in U(x),
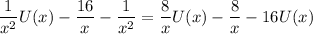
Solve for U(x) :
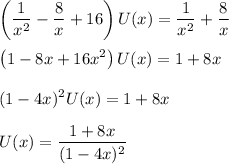
The next step is to get the power series expansion of U(x) so that we can easily identity u(n) as the coefficient of the n-th term in the expansion.
Recall that for |x| < 1, we have
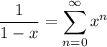
By differentiating both sides, we get
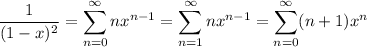
It follows that
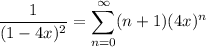
and so

which means