Question

What is the difference quotient for the function f(x) = 8/ 4x + 1

Answer 1

Last option (counting from the top)

Explanation:

For a given function f(x), the difference quotient is:

`(f(x + h) - f(x))/(h) = (1)/(h)*(f(x + h) - f(x))`

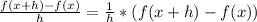
In this case, we have:

`f(x) = (8)/(4x + 1)`

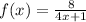
Then the difference quotient will be:

`(1)/(h)*( (8)/(4*(x + h) + 1) - (8)/(4x + 1))`

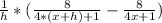
Now we should get a common denominator.

We can do that by multiplying and dividing each fraction by the denominator of the other fraction, so we will get:

`(1)/(h)*( (8)/(4*(x + h) + 1) - (8)/(4x + 1)) = (1)/(h)*((8*(4x + 1))/((4(x + h) +1 )*(4x + 1)) - (8*(4(x + h) + 1))/((4(x + h) +1 )*(4x + 1)))`

Now we can simplify that to get:

`(1)/(h)*(8*(4x + 1) - 8*(4(x + h) + 1))/((4(x + h) +1 )*(4x + 1))} = (1)/(h)*(-32h)/((4(x + h) +1 )*(4x + 1))} = (-32)/((4(x + h) +1 )*(4x + 1))}`

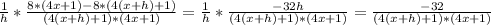
Then the correct option is the last one (counting from the top)