Firstly , before solving the equation , we should know about the chain rule and its formula.
Formula For the Chain rule-
$\rightarrow$ $\sf\dfrac\pink{dy}\pink{dx}$=$\sf\dfrac\pink{dy}\pink{du}$ $\times$ $\sf\dfrac\pink{du}\pink{dx}$ $\leftarrow$
_____________________________
$\sf\huge\underline{\underline{Question:}}$
$\sf\small{Differentiate\: x\: the \:function: (3x² - 9x + 5²)}$
$\sf\huge\underline{\underline{Solution:}}$
$\sf{Let\:y = (3x^2 - 9x + 5)^9}$
$\space$
☆ Differentiating both the sides w.r.t.x using chain rule-
$\mapsto$
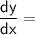
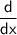
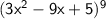
$\space$
$\space$
$\mapsto$
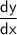 =
=
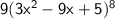

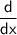 $\sf\small{(3x^2-9+5)}$
$\sf\small{(3x^2-9+5)}$
$\space$
$\space$
$\mapsto$
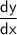 =
=
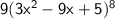

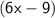
$\space$
$\space$
$\mapsto$
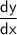 =
=
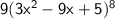 $\times$
$\times$
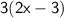
$\space$
$\space$
$\mapsto$
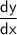 =
=
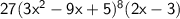
$\space$
$\space$
$\sf\underline\bold\green{❍ dy:dx=27(3x^2-9x+5)^8(2x-3)}$
______________________________