Answer:
The hydrogen sample has a pressure of 0.957 atmospheres.
Step-by-step explanation:
Let consider that the hydrogen sample behaves ideally, the equation of state for ideal gases is:
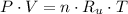 (1)
(1)
Where:
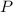 - Pressure, in atmospheres.
- Pressure, in atmospheres.
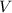 - Volume, in liters.
- Volume, in liters.
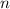 - Molar quantity, in moles.
- Molar quantity, in moles.
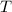 - Temperature, in Kelvin.
- Temperature, in Kelvin.
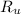 - Ideal gas constant, in atmosphere-liters per mole-Kelvin.
- Ideal gas constant, in atmosphere-liters per mole-Kelvin.
If we know that
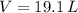 ,
,
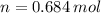 ,
,
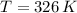 and
and
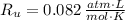 , then the pressure of the hydrogen sample is:
, then the pressure of the hydrogen sample is:
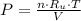
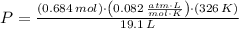
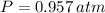
The hydrogen sample has a pressure of 0.957 atmospheres.