Answer:
a) the probability that the defective board was produced during the first hour of operation is
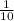 or 0.1000
or 0.1000
b) the probability that the defective board was produced during the last hour of operation is
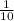 or 0.1000
or 0.1000
c) the required probability is 0.2000
Explanation:
Given the data in the question;
During a specific ten-hour period, one defective circuit board was found.
Lets X represent the number of defective circuit boards coming out of the machine , following Poisson distribution on a particular 10-hours workday which one defective board was found.
Also let Y represent the event of producing one defective circuit board, Y is uniformly distributed over ( 0, 10 ) intervals.
f(y) =
 ; ( a ≤ y ≤ b )
; ( a ≤ y ≤ b )

=
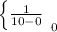 ; ( 0 ≤ y ≤ 10 )
; ( 0 ≤ y ≤ 10 )

f(y) =
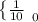 ; ( 0 ≤ y ≤ 10 )
; ( 0 ≤ y ≤ 10 )

Now,
a) the probability that it was produced during the first hour of operation during that period;
P( Y < 1 ) =
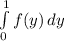
we substitute
=
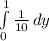
=
![(1)/(10) [y]^1_0](https://img.qammunity.org/2022/formulas/mathematics/college/blzx3wqazztzctf1amhz2pylgc6frmpvef.png)
=
![(1)/(10) [ 1 - 0 ]](https://img.qammunity.org/2022/formulas/mathematics/college/nyq5u6fqek4d08ifvxcwehld0rc2v5irn0.png)
=
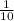 or 0.1000
or 0.1000
Therefore, the probability that the defective board was produced during the first hour of operation is
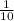 or 0.1000
or 0.1000
b) The probability that it was produced during the last hour of operation during that period.
P( Y > 9 ) =
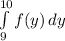
we substitute
=

=
![(1)/(10) [y]^(10)_9](https://img.qammunity.org/2022/formulas/mathematics/college/7hfqmqwtp29z8r745eq88pfqgn8ol3nc51.png)
=
![(1)/(10) [ 10 - 9 ]](https://img.qammunity.org/2022/formulas/mathematics/college/io7ylb1ah3lzuusg2vmijska43omzpz5db.png)
=
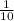 or 0.1000
or 0.1000
Therefore, the probability that the defective board was produced during the last hour of operation is
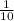 or 0.1000
or 0.1000
c)
no defective circuit boards were produced during the first five hours of operation.
probability that the defective board was manufactured during the sixth hour will be;
P( 5 < Y < 6 | Y > 5 ) = P[ ( 5 < Y < 6 ) ∩ ( Y > 5 ) ] / P( Y > 5 )
= P( 5 < Y < 6 ) / P( Y > 5 )
we substitute
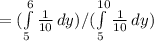
![= ((1)/(10) [y]^(6)_5) / ((1)/(10) [y]^(10)_5)](https://img.qammunity.org/2022/formulas/mathematics/college/ddhqwvrj7vu91hglg3m62z4l5tzmcuie3j.png)
= ( 6-5 ) / ( 10 - 5 )
= 0.2000
Therefore, the required probability is 0.2000