Answer:
1.37 mm²
Step-by-step explanation:
From the image attached below:
Let's take a look at the two rays r and r' hitting the same mirror from two different positions.
Let x be the distance between these rays.
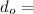 distance between object as well as the mirror
distance between object as well as the mirror
 = distance between mirror as well as the eye
= distance between mirror as well as the eye
Thus, the formula for determining the distance between these rays can be expressed as:
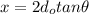
where; the distance between the eye of the observer and the image is:

Then, the tangent of the angle θ is:
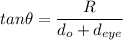
replacing
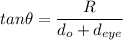 into
into
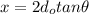 , we have:
, we have:
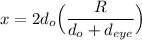
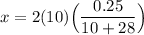
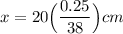
x = (0.13157 × 10) mm
x = 1.32 mm
Finally, the area A = π r²
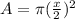
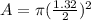
A = 1.37 mm²