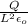Answer:
E_ {total} =
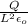
Step-by-step explanation:
In this exercise you are asked to calculate the electric field between two plates, the electric field is a vector
E_ {total} = E₁ + E₂
E_ {total} = 2 E
where E₁ and E₂ are the fields of each plate, we have used that for the positively charged plate the field is outgoing and for the negatively charged plate the field is incoming, therefore in the space between the plates for a test charge the two fields point in the same direction
to calculate the field created by a plate let's use Gauss's law
Ф = ∫ E . dA = q_{int} /ε₀
As a Gaussian surface we use a cylinder with the base parallel to the plate, therefore the direction of the electric field and the normal to the surface are parallel, therefore the scalar product is reduced to the algebraic product.
E 2A = q_{int} / ε₀
where the 2 is due to the surface has two faces
indicate that the surface has a uniform charge for which we can define a surface density
σ = q_{int} / A
q_{int} = σ A
we substitute
E 2A = σ A /ε₀
E = σ / 2ε₀
therefore the total field is
E_ {total} = σ /ε₀
let's substitute the density for the charge of the whole plate
σ= Q / L²
E_ {total} =