Answer:
0.9332
Explanation:
We are given that
Mean diameter,
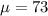
Variance,
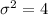
We have to find the probability that the diameter of a selected bearing is less than 76.
Standard deviation,
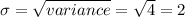
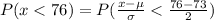
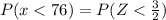
Where
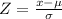
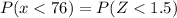
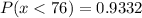
Hence, the probability that the diameter of a selected bearing is less than 76=0.9332