Answer:
Explanation:
Measure of an inscribed angle intercepted by an arc is half of the measure of the arc.
From the picture attached,
m(∠A) =
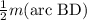
=
![(1)/(2)[m(\text{BC})+m(\text{CD}]](https://img.qammunity.org/2022/formulas/mathematics/high-school/xnuiyvhocpprwg4unwdmuvtf3b90gos56s.png)
=
![(1)/(2)[55^(\circ)+145^(\circ)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/fsvwzpugsx3kj9tnuktholcfhao2rl4tj7.png)
= 100°
m(∠C) =
![(1)/(2)[(360^(\circ))-m(\text{arc BCD})]](https://img.qammunity.org/2022/formulas/mathematics/high-school/h0upma5h5h0hz6rffpx4p0f5s9f41d0jmc.png)
=
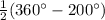
= 80°
m(∠B) + m(∠D) = 180° [ABCD is cyclic quadrilateral]
115° + m(∠D) = 180°
m(∠D) = 65°
m(arc AC) = 2[m(∠D)]
m(arc AB) + m(arc BC) = 2(65°) [Since, m(arc AC) = m(arc AB) + m(arc BC)]
m(arc AB) + 55° = 130°
m(arc AB) = 75°
m(arc ADC) = 2(m∠B)
m(arc AD) + m(arc DC) = 2(115°)
m(arc AD) + 145° = 230°
m(arc AD) = 85°