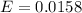Question

Assume that a sample is used to estimate a population proportion p. Find the margin of error E that corresponds to thegiven statistics and confidence level. Round the margin of error to four decimal places.1)99% confidence; n

Answer 1

`E = 0.0158`

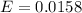
Explanation:

Given

`n = 5900`

`x = 1770`

`CI = 99\%`

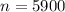
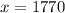
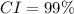
Required

The margin of error (E)

First, calculate proportion p

`p = x/n`

`p = 1770/5900`

`p = 0.3`

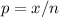
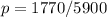
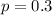
Given that:

`CI = 99\%`

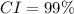
Calculate the alpha leve;

`\alpha = 1 - CI`

`\alpha = 1- 0.99`

`\alpha= 0.01`

Divide by 2

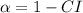
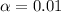
`\alpha/2= 0.01/2`

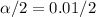
Subtract from 1

`1 - \alpha/2= 1 - 0.01/2`

`1 - \alpha/2= 0.995`

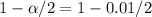
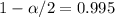
The corresponding z value is:

`z =2.576`

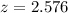
So, the margin of error is:

`E = z * √(p * (1 - p)/n)`

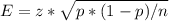
So, we have:

`E = 2.576 * √(0.3 * (1 - 0.3)/5600)`

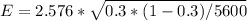
Using a calculator, we have:

`E = 0.01577471394`

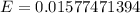
Approximate

`E = 0.0158`