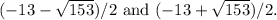The correct solutions for the equation
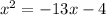 are
are
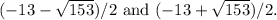
To find the solutions of the quadratic equation \(ax^2 + bx + c = 0\), you can use the quadratic formula:
![\[ x = (-b \pm √(b^2 - 4ac))/(2a) \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/dykbynok2shwklm89mcx36t77uhe9mijt1.png)
In the given equation \(x^2 = -13x - 4\), the coefficients are \(a = 1\), \(b = 13\), and \(c = 4\). Substituting these values into the quadratic formula, you get:
![\[ x = (-13 \pm √(13^2 - 4(1)(-4)))/(2(1)) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/9157i9m450e41m0l989djpdea9mpanweg3.png)
Simplifying further:
![\[ x = (-13 \pm √(169 + 16))/(2) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ttuvt1tu2gdet2v5crhwv57lm1kq433ull.png)
![\[ x = (-13 \pm √(185))/(2) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/tnb19nt0qd5fp6ur5ynqj2esr3j5wam0qt.png)
Therefore, the solutions are:
![\[ x = (-13 - √(185))/(2) \] and x = (-13 + √(185))/(2) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/1qwwfszt42q0sjskdnqk9il2nfntczhyzv.png)
Simplifying the radicals, you get:
![\[ x = (-13 - √(153))/(2) \] x = (-13 + √(153))/(2) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/mta76r4swthnjkscn48hxsbexag5nr47rk.png)
So, the correct solutions are