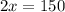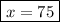1 Answer

Tomvodi · Answer 1 · 2022-11-09T15:28:49+0000

It looks like the equation is

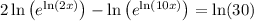
$2\ln\left(e^(\ln(2x))\right)-\ln\left(e^(\ln(10x))\right) = \ln(30)$

Right away, we notice that any solution to this equation must be positive, so x > 0.

For any base b, we have
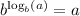$b^(\log_b(a))=a$ , so we can simplify this to

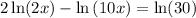
$2\ln(2x)-\ln\left(10x\right) = \ln(30)$

Next,
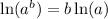$\ln(a^b)=b\ln(a)$ , so that

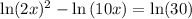
$\ln(2x)^2-\ln\left(10x\right) = \ln(30)$

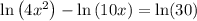
$\ln\left(4x^2\right)-\ln\left(10x\right) = \ln(30)$

Next,
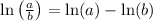$\ln\left(\frac ab\right)=\ln(a)-\ln(b)$ , so that

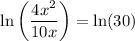
$\ln\left((4x^2)/(10x)\right) = \ln(30)$

For x ≠ 0, we have
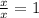$\frac xx=1$ , so that

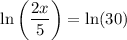
$\ln\left(\frac{2x}5\right) = \ln(30)$

Take the antilogarithm of both sides:

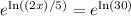
$e^(\ln\left((2x)/5\right)) = e^(\ln(30))$

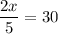
$\frac{2x}5 = 30$

Solve for x :

2x = 150

$\boxed{x=75}$

Please log in or register to add a comment.