Question

If x = 1, y = 7, and z = 15, determine a number that when added to x, y, and z yields

consecutive terms of a geometric sequence. What are the first three terms in the
geometric sequence?

Answer 1

The first three terms in the geometric sequence are 18, 24, 32.

Explanation:

A number when added to
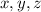`x,y,z` that yields consecutive terms of a geometric sequence is an unknown number
`t\in \mathbb{Z}`

Given

`x = 1, y = 7, z = 15`

We know

`\alpha _1 = 1+t`

`\alpha _2 = 7+t`

`\alpha _3 = 15+t`

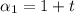
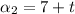
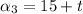
Recall that a geometric sequence is in the form

`\boxed{a_n = a_1 \cdot r^(n-1)}`

Therefore, once
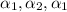`\alpha_1, \alpha_2, \alpha_1` are consecutive terms,

`15+t = (1+t) r^(3-1) \implies 15+t = (1+t) r^2`

To find the ratio, for

`\dots a_(k-1), a_k, a_(k+1) \dots`

we know

`(a_k)/(a_(k-1)) =(a_k)/(a_(k-1)) =r`

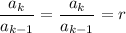
Therefore,

`((7+t))/((1+t)) =((15+t))/((7+t)) \implies (7+t)^2 = (15+t)(1+t)`

`\implies 49+14t+t^2=15+16t+t^2 \implies -2t=-34 \implies t=17`

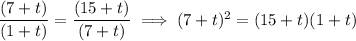
The ratio is therefore

`r=(4)/(3)`

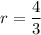
Therefore, the first three terms in the geometric sequence are 18, 24, 32.