Answer:
The first three terms in the geometric sequence are 18, 24, 32.
Explanation:
A number when added to
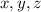 that yields consecutive terms of a geometric sequence is an unknown number
that yields consecutive terms of a geometric sequence is an unknown number

Given
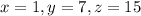
We know
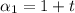
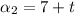
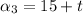
Recall that a geometric sequence is in the form

Therefore, once
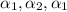 are consecutive terms,
are consecutive terms,

To find the ratio, for

we know
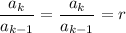
Therefore,
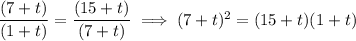
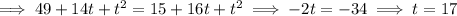
The ratio is therefore
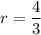
Therefore, the first three terms in the geometric sequence are 18, 24, 32.