Question

Find the area of the shaded region. Round your answer to the nearest hundredth.

Answer 1

Explanation:

The formula for finding the area of a pentagon(regular) given 1 side is

A =
`(1)/(4)\sqrt{5(5+2√(5))}s^(2)\)`

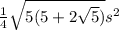
s (the side) = 12

Area =
`(1)/(4)\sqrt{5(5+2√(5))}12^(2)\)`

Area =
`(1)/(4)\sqrt{5(5+2√(5))}144\)`

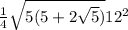
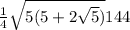
Area = sqrt(5(5 + 2*2.2361) * 36

Area = sqrt(5( 5 + 4.4721)) * 36

Area = sqrt(5*9.4721) * 36

Area = sqrt(47.3606) * 36

Area = 6.882 * 36

Area = 247.7485

The area of the circle = pi r*2 but we don't have r.

If you know any trig, the formula for the radius of the circle is

R = s/(2*sin(180)/n) n = 5 because you are using a 5 sided figure.

R = 12/(2*sin(180/5)

R = 12/2* sin(36)

R = 6 / sin(36)

R = 10.207

So the area of the circle is pi * R^2

Area = 3.14 * 10.2078^2

Area = 327.1854

The area of the shaded part is the difference between the 2 areas we found

Answer: 327.1854 - 247.7485

Answer: 79.44