Question

Casey's phone service charges a flat monthly fee of $30 for the first 1000 minutes of calls and $0.40 per minute over 1000. Determine Casey's monthly charge if he makes 1,100 minutes of calls?

Answer 1

Casey's monthly charge for making 1,100 minutes of calls is $70.

Explanation:

We can write a piecewise function to model the situation.

Since Casey's phone service only charges a monthly fee of $30 for the first 1000 minutes, we can write that for calling t minutes:

`\displaystyle C(t) = 30\text{ if } t\leq 1000`

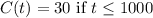
In other words, the total cost is only $30 is the total minutes of call is less than 1000 minutes.

However, if the total minutes of calls is greater than 1000, then its $0.40 per minute on top of the 30. Thus:

`\displaystyle C(t) = 30 + 0.4(t-1000)\text{ if } t>1000`

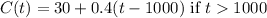
All together, our piecewise function will be:

`\displaystyle C(t) = \begin{cases} 30 & t\leq 1000 \\ 30 + 0.4(t-1000) & t>1000\end{cases}`

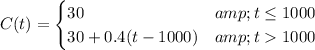
We want to determine Caseys monthly charge if he makes 1,100 minutes of calls. So, t = 1100. Since 1100 > 1000, we will use the second equation. This yields:

`C(1100)= 30+0.4((1100)-1000)`

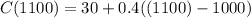
Evaluate:

`\displaystyle C(1100) = 30+0.4(100) = 30+40=\$70`

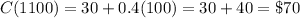
Casey's monthly charge for using 1,100 minutes of call is $70.