Question

If y = ax^2 + bx + c passes through the points (-3,10), (0,1) and (2,15), what is the value of a + b + c?

Answer 1

Hi there!

`\large\boxed{a + b + c = 6}`

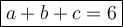
We can begin by using the point (0, 1).

At the graph's y-intercept, where x = 0, y = 1, so:

1 = a(0)² + b(0) + c

c = 1

We can now utilize the first point given (-3, 10):

10 = a(-3)² + b(-3) + 1

Simplify:

9 = 9a - 3b

Divide all terms by 3:

3 = 3a - b

Rearrange to solve for a variable:

b = 3a - 3

Now, use the other point:

15 = a(2)² + 2(3a - 3) + 1

14 = 4a + 6a - 6

Solve:

20 = 10a

2 = a

Plug this in to solve for b:

b = 3a - 3

b = 3(2) - 3 = 3

Add all solved variables together:

2 + 3 + 1 = 6