Question

Find the distance traveled by a particle with position (x, y) as t varies in the given time interval.

x = 3 sin^2(t), y = 3 cos^2(t), 0< t<3pi
What is the length of the curve?

Answer 1

The length of the curve (and thus the total distance traveled by the particle along the curve) is

`\displaystyle\int_0^(3\pi)√(x'(t)^2+y'(t)^2)\,\mathrm dt`

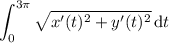
We have

x(t) = 3 sin²(t ) ==> x'(t) = 6 sin(t ) cos(t ) = 3 sin(2t )

y(t) = 3 cos²(t ) ==> y'(t) = -6 cos(t ) sin(t ) = -3 sin(2t )

Then

√(x'(t) ² + y'(t) ²) = √(18 sin²(2t )) = 18 |sin(2t )|

and the arc length is

`\displaystyle 18 \int_0^(3\pi) |\sin(2t)| \,\mathrm dt`

Recall the definition of absolute value: |x| = x if x ≥ 0, and |x| = -x if x < 0.

Now,

• sin(2t ) ≥ 0 for t ∈ (0, π/2) U (π, 3π/2) U (2π, 5π/2)

• sin(2t ) < 0 for t ∈ (π/2, π) U (3π/2, 2π) U (5π/2, 3π)

so we split up the integral as

`\displaystyle 18 \left(\int_0^(\pi/2) \sin(2t) \,\mathrm dt - \int_(\pi/2)^\pi \sin(2t) \,\mathrm dt + \cdots - \int_(5\pi/2)^(3\pi) \sin(2t) \,\mathrm dt\right)`

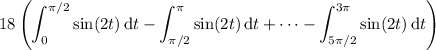
which evaluates to 18 × (1 - (-1) + 1 - (-1) + 1 - (-1)) = 18 × 6 = 108.