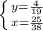Question

2x+8y=3 and 4x-3y=2 value of x and y.. plzz help me​

Answer 1

Set a system of equations:

`\left \{ {{2x+8y=3} \atop {4x-3y=2}} \right.`

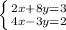
Multiply the whole upper equation by 2 and the whole bottom equation by 1 so their x-value equals:

`\left \{ {{2(2)x+8(2)y=3(2)} \atop {4(1)x-3(1)y=2(1)}} \right.\\\\=\left \{ {{4x+16y=6} \atop {4x-3y=2}} \right.`

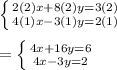
Subtract the upper equation by the bottom equation & solve for y:

`(4x-4x)+(16y-(-3y))=6-2\\\\19y=4\\\\y=(4)/(19)`

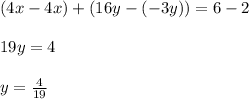
Substitute in the y-value to a equation to find x:

`2x+8y=3\\\\2x+8((4)/(19) )=3\\\\2x=3-(32)/(19) =(57)/(19) -(32)/(19) =(25)/(19) \\\\x=((25)/(19))/(2) =(25)/(19)*(1)/(2) =(25)/(38)`

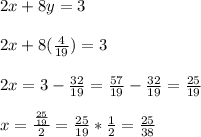
Therefore, the answer would be:

`\left \{ {{y=(4)/(19) } \atop {x=(25)/(38) }} \right.`