Question

There is given an ideal capacitor with two plates at a distance of 3 mm. The capacitor is connected to a voltage source with 12 V until it is loaded completely. Then the capacitor is disconnected from the voltage source. After this the two plates of the capacitor are driven apart until their distance is 5 mm. Now a positive test charge of 1 nC is brought from the positively charged plate to the negatively charges plate. How large is the kinetic energy of the test charge? The test charge of 1 nC can be regarded to be so small that it does not influence the electric field between the two plates of the capacitor.

Answer 1

The kinematic energy of the positive charge is 2 10⁻⁸ J

This electrostatics exercise must be done in parts, the first part: let's start by finding the charge of the capacitor, the capacitance is defined by

C =
`(Q)/(\Delta V)`

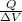
C = ε₀
`(A)/(d)`

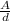
we solve for the charge (Q)

`(Q)/(\Delta V) = \epsilon_o (A)/(d)`

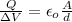
indicates that for the initial point d₁ = 3 mm = 0.003 m and the voltage is DV₁ = 12

Q =
`\epsilon_o \ (A \ \Delta V_1 )/(d_1)`

Now the voltage source is disconnected so the charge remains constant across the ideal capacitor.

For the second part, the condenser is separated at d₂ = 5mm = 0.005 m

Q = \epsilon_o \ \frac{A \ \Delta V_2 }{d_2}

we match the expressions of the charge and look for the voltage

`(\Delta V_1)/(d_1) = (\Delta V_2)/(d_2)`

ΔV₂ =
`(d_2)/(d_1 ) \ \Delta V_1`

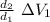
The third part we use the concepts of conservation of energy

starting point. With the test load (q = 1 nC = 1 10⁻⁹ C) next to the left plate

Em₀ = U = q DV₂

Em₀ = q \frac{d_2}{d_1 } \ \Delta V_1

final point. Proof load on the right plate

Em_f = K

energy is conserved

Em₀ = em_f

q \frac{d_2}{d_1 } \ \Delta V_1 = K

we calculate

K = 1 10⁻⁹ 12
`(0.005)/(0.003)`

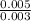
K = 20 10⁻⁹ J

In this exercise, as the conditions at two different points of separation give, the area of ​​the condenser is not necessary and with conservation of energy we find the final kinetic energy of 2 10⁻⁸ J