Answer:
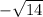 in the lower right corner
in the lower right corner
===========================================================
Step-by-step explanation:
A rational number is any fraction like 2/3 or 7/9. Pick any two integers, divide them, and you get a rational number. Zero cannot be in the denominator.
Based on that, we can see that 129/999 is rational, which is crossed off the list of potential answers.
Furthermore,
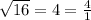 is also rational since we can form a fraction of integers. Cross this off the list as well. Always try to simplify the expression as much as possible.
is also rational since we can form a fraction of integers. Cross this off the list as well. Always try to simplify the expression as much as possible.
-----------------
When converting a fraction to decimal form, it turns out that any rational number has either two cases:
- The decimal terminates or stops (eg: 1/2 = 0.5)
- The decimal pattern repeats forever (eg: 2/99 = 0.02020202...)
This means the number
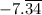 = -7.3434343434... is also rational, which is crossed off the list also.
= -7.3434343434... is also rational, which is crossed off the list also.
----------------
The only thing left is
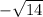 which is not rational, and therefore we consider it irrational. We cannot form a fraction of integers to represent this square root value. Note how 14 is not a perfect square.
which is not rational, and therefore we consider it irrational. We cannot form a fraction of integers to represent this square root value. Note how 14 is not a perfect square.