The differential equation
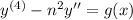
has characteristic equation
r ⁴ - n ² r ² = r ² (r ² - n ²) = r ² (r - n) (r + n) = 0
with roots r = 0 (multiplicity 2), r = -1, and r = 1, so the characteristic solution is

For the non-homogeneous equation, reduce the order by substituting u(x) = y''(x), so that u''(x) is the 4th derivative of y, and
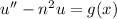
Solve for u by using the method of variation of parameters. Note that the characteristic equation now only admits the two exponential solutions found earlier; I denote them by u₁ and u₂. Now we look for a particular solution of the form
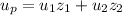
where

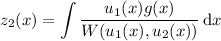
where W (u₁, u₂) is the Wronskian of u₁ and u₂. We have

and so
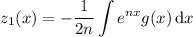
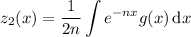
So we have
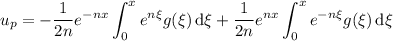
and hence
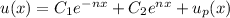
Finally, integrate both sides twice to solve for y :
