That's a question about quadratic function.
Any quadratic function can be represented by the following form:
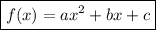
Example:
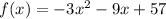 is a function where
is a function where
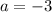 ,
,
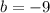 and
and
 .
.
Okay, in our problem, we need to find the value of x when
 . That's mean that the result of our function is equal to zero. Therefore, we have the quadratic equation below:
. That's mean that the result of our function is equal to zero. Therefore, we have the quadratic equation below:

To solve a quadratic equation, we use the Bhaskara's formula. Do you remember the value of a, b and c? They going to be important right now. This is the Bhaskara's formula:
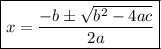
So, let's see the values of a, b and c in our equation and apply them in the Bhaskara's formula:
In
 equation,
equation,
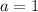 ,
,
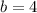 and
and
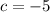 . Let's replace those values:
. Let's replace those values:
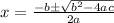

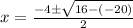

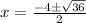
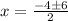
From now, we have two possibilities:
To add:
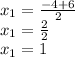
To subtract:

Therefore, the result of our problem is:
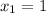 and
and
 .
.
I hope I've helped. ^^
Enjoy your studies. \o/