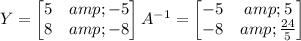Question

How to solve the matrix equation for matrix Y.simplify all elements


`Y\left[\begin{array}{ccc}-1&-4\\0&-5\\\end{array}\right] = \left[\begin{array}{ccc}5&-5\\8&8\\\end{array}\right]`

Answer 1

Given YA = B, you can solve for Y by multiplying by A ⁻¹ on the right (on both sides of the equation). So we have

YA = B ==> (YA) A ⁻¹ = BA ⁻¹ ==> Y (AA ⁻¹) = BA ⁻¹ ==> Y = BA ⁻¹

provided that the inverse of A exists. In this case, det(A) = 5 ≠ 0, so the inverse does exist, and

`A=\begin{bmatrix}-1&-4\\0&-5\end{bmatrix} \implies A^(-1)=\frac1{\det(A)}\begin{bmatrix}-5&0\\4&-1\end{bmatrix} = \begin{bmatrix}-1&0\\\frac45&-\frac15\end{bmatrix}`

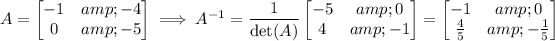
Then

`Y=\begin{bmatrix}5&-5\\8&-8\end{bmatrix}A^(-1) = \begin{bmatrix}-5&5\\-8&\frac{24}5\end{bmatrix}`