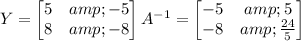Given YA = B, you can solve for Y by multiplying by A ⁻¹ on the right (on both sides of the equation). So we have
YA = B ==> (YA) A ⁻¹ = BA ⁻¹ ==> Y (AA ⁻¹) = BA ⁻¹ ==> Y = BA ⁻¹
provided that the inverse of A exists. In this case, det(A) = 5 ≠ 0, so the inverse does exist, and
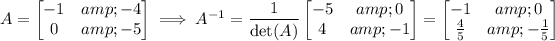
Then