Answer:
The speed of the object when displacement is 0.041 meters is 0.375 meters per second.
Step-by-step explanation:
First, we need to determine the angular frequency of the system (
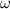 ), in radians per second:
), in radians per second:
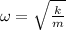 (1)
(1)
Where:
 - Spring constant, in newtons per meter.
- Spring constant, in newtons per meter.
 - Mass, in kilograms.
- Mass, in kilograms.
If we know that
 and
and
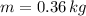 , then the angular frequency of the system is:
, then the angular frequency of the system is:
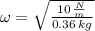

The kinematic formulas for the position (
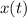 ), in meters, velocity (
), in meters, velocity (
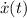 ), in meters per second, and acceleration of the object (
), in meters per second, and acceleration of the object (
 ), in meters per square second, are:
), in meters per square second, are:
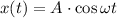 (2)
(2)
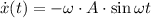 (3)
(3)
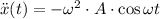 (4)
(4)
Where
 is the amplitude of the motion, in meters.
is the amplitude of the motion, in meters.
From (2) we determine the time associated with position
 (
(
 ,
,
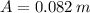 ):
):
 (5)
(5)
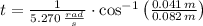
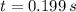
And the speed of the object is:
![\dot x(t) = -\left(5.270\,(rad)/(s) \right)\cdot (0.082\,m)\cdot \sin \left[\left(5.270\,(rad)/(s) \right)\cdot (0.199\,s)\right]](https://img.qammunity.org/2022/formulas/physics/high-school/f4r0ndgwiyl58ctsw3sel6fn1oxdsea1ib.png)
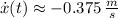
The speed of the object when displacement is 0.041 meters is 0.375 meters per second.