9514 1404 393
Answer:
x = √2
Explanation:
A graph indicates the only solution is near x=√2.
__
Square both sides, separate the radical and do it again.
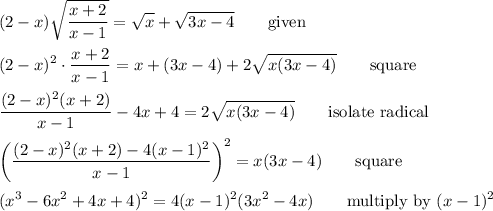
Now, we can put this polynomial equation into standard form and factor it.
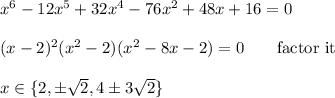
The original equation requires that we restrict the domain of possible solutions. In order for the radicals to be non-negative, we must have x ≥ 4/3. In order for the left side of the equation to be non-negative, we must have x ≤ 2. So, the only potential solutions will be in the interval [4/3, 2].
The only values in the above list that match this requirement are {√2, 2}. We know that the right side of the equation cannot be zero, so the value x=2 is also an extraneous solution.
The only solution is x = √2.
_____
Additional comment
For solving higher-degree polynomials, I like to use a graphing calculator to help me find the roots. The second attachment shows the roots of the 6th-degree polynomial. They can help us factor the equation. (There are also various machine solvers available that will show factors and roots.)